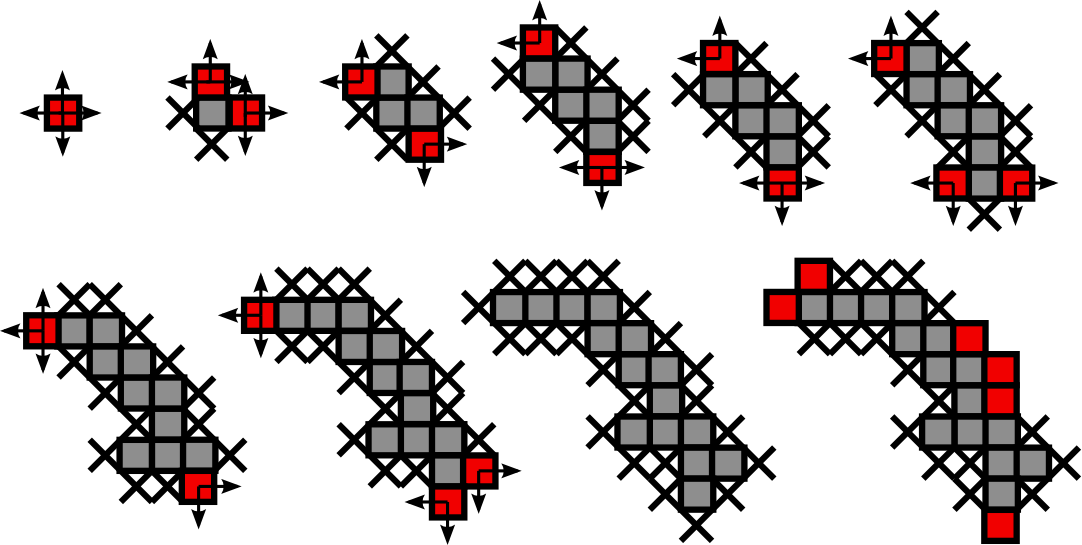
Problem metadynamiky
Metadynamika sampluje nekolikanasobne body ktere uz ma jednou nasamplovane. To ji cini neefektivni v techto ohledech:
- V kazdem kroku se sumuje prez mnoho gaussianu (vsechny zatim ulozene)
- Energie systemu se vyhodnocuje (tzn. napr. ab-initio vypocet) se provadi opakovane i v oblastech potencialovych jam kde uz byla energie dobre nasamplovana
Predpoklady
Metadynamika tak jako tak spoleha na tyto predpoklady
- Energeticky profil je dostatecne hladky aby jej stacilo vzorkovat s rozlisenim dX, kde dX je polosirka pokladanych gaussianu
- Mnozina X pro ktere je E(X)< Emax je dost mala v prostoru {X} na to aby ji bylo mozne celou pokryt nejakym rozumne malym poctem gaussianu se stredem v Xi a polosirkou dX.
Diskretizace Xi
V klasicke metadynamice muze byt Xi - tj. poloha vzorku v kterem vyhodnocujeme E(Xi) a do ktereho pokladame gaussian Gi - libovolny nahodny vektor realnych cisel. Vyuzijeme-li ale predpokladu o hladkosti E(X), muzeme E(X) stejne dobre vzorkovat i gausiany pokladanymi jen do diskretnich pozic s vzajmne pravidelnymi rozestupy (umyslne se vyhybam pojmu mrizka). Gaussiany s konecnou polosirkou dX nemohou samplovat PES presneji at uz jsou rozlozeny spojite, nebo jen diskretne s rozestupy ~dX.
Pzn. Pojmu mrizka se vyhybam proto ze ve vicedimenzionalnim prostoru ktery predpokladame se jakakoli mrizka stava velmi pametove nakladnou (m^N, kde m je pocet vzorku v kazde dimenzi). Tato diskretizace ovsem nevyzaduje alokovat pamet pro polohy X ktere zatim nebyly samplovany (a pravdepdoobne ani nebudou). Stejne jako v pripade puvodni Metadynamiky si pamatujeme pouze body, ktere uz samplovany byly (a kterych je tudis relativne maly pocet), prezto defakto tyto zapamtovane body tvori neuplnou mrizku.
Vyhody diskretizace
Redukce poctu gaussianu - Nejjednoduzsi a nejprimocarejsi vyhoda te ta, ze namisto abychom v dX-okoli kazdeho bodu Xi meli nekolik (obvykle desitky) prekryvajicich se gausianu, mame nyni pouze jeden gaussian v bode Xi, jehoz vysku mame naskalovanou poctem vzorku ktere jsme v tomto bode provedli.
Diky tomu neni treba se jakkoli zdrahat akumulovat “flooding” potencial v kazdem kroku dynamiky, nijak tim totiz nezvysujeme pocet gaussianu ktere by bylo treba vyhodnocovat. V klasicke metadynamice muze predstavovat pocet gaussianu problem, proto se obvykle namisto pridani maleho gausianu v kazdem kroku pridava vetsi gaussian jednou za nekolik kroku. To ovsem vede k mene hladkemu vzorkovani.
Redukce poctu vyhodnoceni v kazdem kroku - Vzhledem k tomu, ze gaussianu v klasicke metadynamice maji neomezeney dosah (nemaji kompaktni nosic) scitame stovky gaussianu z nichz vetsina v podstate neprispiva k hodnotam meta-PES v bode Xi protoze jejich stredy Xj se nachazi podstatne dale nez je jejich polosirka dX. V diskretizovane verzi je mozne misto gausianu pouzivat napr. kubicky spline s kompaktnim nosicem. Diky tomu muzeme vyhodnocovat jen nekolik bazovych funcki pro bod Xi relevantnich, navic tyto bazove funkce aproximuji PES presneji.
Redukce poctu vyhodnoceni E(X) - Predpokladame-li ze provadime molekularni dynamiku velkeho systemu, nebo ab-initio molekularni dynamiku, nepredstavuje pocet ulozenych resp. vyhodnocovanych gaussianu velky problem, protoze nakladnost vyhodnocemi E(Xi) ze stavu systemu Xi je mnohem vetsi. V tomto pripade je ovsem velmi neefektivni vyhodnocovat hodnoty E(X) v bodech lezicich v oblastech ktere uz byly huste nasamplovany (kde lezi mnoho gaussianu). Podle predpokladu o hladkosti E(X) je mozne dobre aproximovat E(Xi) hodnotami E(Xj) uz spoctenymi v predeslych krocich. Proto je vyhodne uchovavat si spolu s vahami flooding potencialu (tj. wahami Wi gausianu Gi) take hodnoty Ei. Podobne pak jine veliciny uzitecne pro beh molekulrane dynamicke simulace, napr. gradienty resp. hessiany.
V pripade ze mame ulozenu tuto informaci, nepotrebujeme defakto pro MD kroky uvnitr uz navzorkovanych casti PES (tj. uvnitr minim) vubec vyhodnocovat E(X) ab-initio. Muzeme propagovat celou molekularni dynamiku ciste jen na zaklade ulozenych hodnot, a E(X) vyhodnotit jen ve vzacnem pripade kdy system dorazi k hranice navzorkovane oblasti.
Pametova narocnost takoveho postupu neni nijak dramaticka. Jestlize predpokladame typickou dimenzionalitu order parametru podle ktereho provadime metadynamiku N = 6..10 (vice neni prekticky zvladnutelnych kvuli poctu vzorku) a nekolik stovek resp. ticic vzorku (vice neni zvladnutelne kvuli dobe vyhodnocovani E() v kazdem kroku) potom nam staci ulozit 6..10 tisic cisel pro gradienty resp. 36-100 tisic cisel pro hesiany. To je pro pamet dnesich pocitacu zanedbatelne. Dokonce i v pripade ze bychom si chteli uchovavat uplny gradient nebo dokonece hesian celho systemu neni to tak strasne. Dejme tomu ze pocet stupnu volnosti celeho systemu je 1000. Gradienty predstavuji 1 milion cisel coz je stale jen stale jen nekolik MB pameti, dokonce i hessian s bude predstavovat jen 1GB pameti, ale ukladani celeho hesianu je malo ucelene. Ukladany by mely byt budto jen diagonalni komponenty, nebo nejaka vhodne komprimovana forma.
Total flooding
Obvyklou aplykaci metadynamiky je:
- a] Navzorkovani tvaru PES
- b] Spocteni termodinamickych strednich hodnot nejakeho operatoru
- c] Nalezeni nejnizsiho tranzitniho stavu uniku z daneho minima
Pro prvni dve aplikace a],b] zjevne potrebujeme spise Totalni hodnotu E(Xi) v jednotlivych ekvidistatne rozlozenych bodech nez sumu malych gaussianku Gi konstantni vysky Wi. Z tohoto hlediska je tedy vyhodne ze mame vzorkovaci body Xi rovnomerne rozlozene, cimz zajistujeme ze elementy dVi v pripadnem integralu budou dobre definovane. Vyhodne by dale bylo zaplavit bod Xi ihned (v prvnijm kroku) jeho totalni hodnotou E(Xi) tak aby vysledky meta-E(Xi) = 0 a dale se timto bodem nezabyvat (tento bod by se dostal energeticky pekne vysoko). To vsak neni mozne ze dvou duvodu.
- Bod Xi by pak predstavoval barieru pro prechod do opacne casti stavoveho prostoru
- Toto neni aplikovatelne pro hledani nejnizsiho minima
Reseni se nabizi: V praxi nam nic nenarizuje abychom v bode Xi pouzivali meta-E() danou poctem akumulovanych vzorku. Muzeme si v tomto bode stanovit meta-E() presne takovou jaka se nam bude hodit. Pro potreby hledani nejnizsiho trenzitniho stavu ( ad c] ) je nejucelnejsi aby meta-PES byl vsude v navzorkovanych oblastech vsude presne konstatni - to je take idealni limitni stav ke kteremu se snazime v klasicke meta-Dynamice priblizit napr. tim ze volime dostatecne nizke Wi a zajistujeme tak ze Gi budou vyplnovat potencialovou jamu co nejrovnomerneji. Total flooding metadynamika se tedy zaklada na tom ze ke konstrukci meta-PES vubec nepouzivame akumulovane hodnoty gaussianu. Proste si urcime nejakou prahovou hodnotu energie E_min. A vsude v nasamplovanych oblastech kde byla energie mensi nez E_min nastavime meta-PES = E_min. System se tak v teto oblasti pohybuje zcela bez potencialu, a zcela bez vyhodnocovani E() popr. sil ab-initio. Rychle dorazi k okraji, a teprve zde muze sklouznout do energiticky nizsi pozice E(Xi)<E_min, protoze zde jeste nebyl ulozen zadny vzorek (jeste nebyla zaplavena). V pripade ze se castice pohybuje v jame s E_min dost dlouho aby navzorkovala okraje (cimz se ujistime ze jsme nasli vsechny tranzitni stavy s energii mensi nez E_min) tak zvysime E_min o patricky inkrement pro vsechny uz navzorkovane body.
Border Methadynamics
Total floodin odhaluje hlavni nedostatek smetadynamiky - vetsinu kroku se nedeje nic poidstatneho - system se pouze mota uvnitr uz navzorkovane oblasti aniz by odhalovou jakoukoli novou informaci. Je to samozdrejme lepsi nez v normalni dynamice, kde se v teto oblasti mota jeste neskonale (blotzmanovskym faktorem nasobeno) dele, ale ani tak to neni idealni. Problem se stava mnohem mensim kdyz namisto vyhodnocovani E() a sil F() ab initio pozuvame ulozene hodnoty, ale porad to neni uplne ono. Vzdyt prece vsechno relevantni se odehrava pouze na hranicich uz nasamplovane oblasti. Proc tedy nevzorkujeme pouze v teto oblasti? Pokusme se navrhnout takovy algoritmus. Mame tedy databazi predchozich vzorku, v nichz vime ze energie byla mensi nez E_min. Tuto databazi muzeme rozdelit na dve kategorie:
- a]Vnitrni body - pro nas bezcene ktere bychom nechteli samplovat znova
- b]Body hranicni, v jejichz bezprostredni blizkosti se muze nachazet dalsi cast mnoziny Xi takovych ze E(Xi)<E_min, nebo dokonce hledany tranzitni stav.
Musime tedy vymyslet zpusob jak
- Rozlisit body hranicni
- Jak prohledat jejich okoli
- Jak zajistit abychom nejprve nasli nejnizsi tranzitni stavy
ad 1] Hranicni body rozlisime snadno - tento bod nema alespon jednoho nejblizsiho souseda ( predstavme si mrizku kterou defakto postupne konstruujeme) Tato najivni uvaha ma ale jednen hacek - Musime si uvedomit ze pracujeme v N rozmernem prostoru. Jak jsme rekli N neni moc velke (6..10) ale prezto pocet nejblizsich sousedu roste jako 2^N. Nebylo by vubec efektivni kolem kazdeho bodu Xi testovat napr. 2^10 = 1024 sousednich bodu. Omezme se proto na nejblizsi sousedy kteri lezi v nekterem ortogonalnim smeru napr. (x+1,y),(x-1,y),(x,y+1),(x,y-1) ale nikoli (x+1,y+1). Tj vezmeme pouze body na mrizce ktere maji spolecne rozhrani, nikoli diagonalni sousedy. Takovych bodu je jen 2N. ad 2] Prohledavani okoli je ekvivalentni hledani nejblizsiho souseda. Opet vezmeme pouze 2N ortogonalnich sousednich pozic, v kterych jeste nebyl proveden vzorek. ad 3] Abychom zajistili ze nejprve najdeme nejnizsi tranzitni stav staci vybrat hranicni bod s nejnizsi energii.
Jeste poznamka - protoze nase mnozina navzorkovanych hodnot tvori obvykle tenkou linii nebo podobny nekompaktni utvar v mnoharozmernem prostoru je povrch utvaru velmi velky oproti objemu, jinymi slovy pocet bodu lezicich na povrchu je obvykle mnohem vetsi nez pocet bodu lezicich uvnitr. Klasicka Metadynamika ovsem spoleha na to ze energie resp. gradienty (Sily) vetsiny techto bodu budou priliz nepriznive a system je vubec nebude prochazet. V nasem algoritmu bychom toto meli postihnout take - smysluplne hrnicni body jsou pouze ty ktere maji vedle sebe “volne policko” ktere neni nasamplovane, ale zaroven gradient do nej smerujici neni priliz vysoky (!). V opacnem pripade bychom zbytecne straceli cas pokusy samplovat nesmyslne hranicni body ktercyh je vetsina. Odhad predpokladane energie bodu na zakladne gradientu plati dokud plati nas predpoklad o dostatecne hladkosti PES. Ve vysledku mame tedy 3 kategorie bodu:
- a] Vnitrni body - uz nasamplovane E < E_min, a vsichni ortogonalni sousede bud existuji (jsou nasamplovani), nebo jsou zakazani (priliz vysoky gradient)
- b] Hranicni body - uz je nasamplovan, E < E_min, a v okoli lezi nejake volne policko ktere nasamplovano nebylo, a toto policko neni zakazane
- c] Zakazane body - body ktere budto uz byly nasamplovany, nebo jejich predpokladana energie (podle gradientu resp. hesianu) je priliz vysoka.
Vysledny algorismus
- 1] Vyhodnot E(X0) a gradient F(X0), X0 je vychozi a zaroven hranicni bod
- 2] zvol energii pocatecni E_min > E(X0)
- 3] Prohledej ortogonalni sousedni policka X0 v poradi od nejnizsi energie, pokud predpokladana energie neni priliz vysoka (>E_min)
- 4] Pro kazdeho navzorkovaneho souseda si uloz zda je hranicnim bodem a zda v jeho okoli lezi zakazane body
- 5] Az budou vsichni sousede X0 navzokrovani nebo oznaceni za zakazane oznac X0 za vnitrni
- 6] Vem hranicni bod s nejnizsi E(Xi) a prohledej jeho sousedy (rozdel je na Hranicni, vnitrni a zakazane), pak ho oznac za vnitrni
- 7] Vem dalsi energeticky nejnizsi hranicni bod ……..
- 8] Az vycerpas vsechny hranicni body (tj. zustanou budto navzorkovane vnitrni na jejichz povrchu budou zakazane) zvys E_min
- 9] Pro vsechny zakazane body vyhodnot zda jejich predpokladane energie nejsou mensi nez nove E_min, ty co jsou nastav jako hranicni.
- 10 - go to 6]