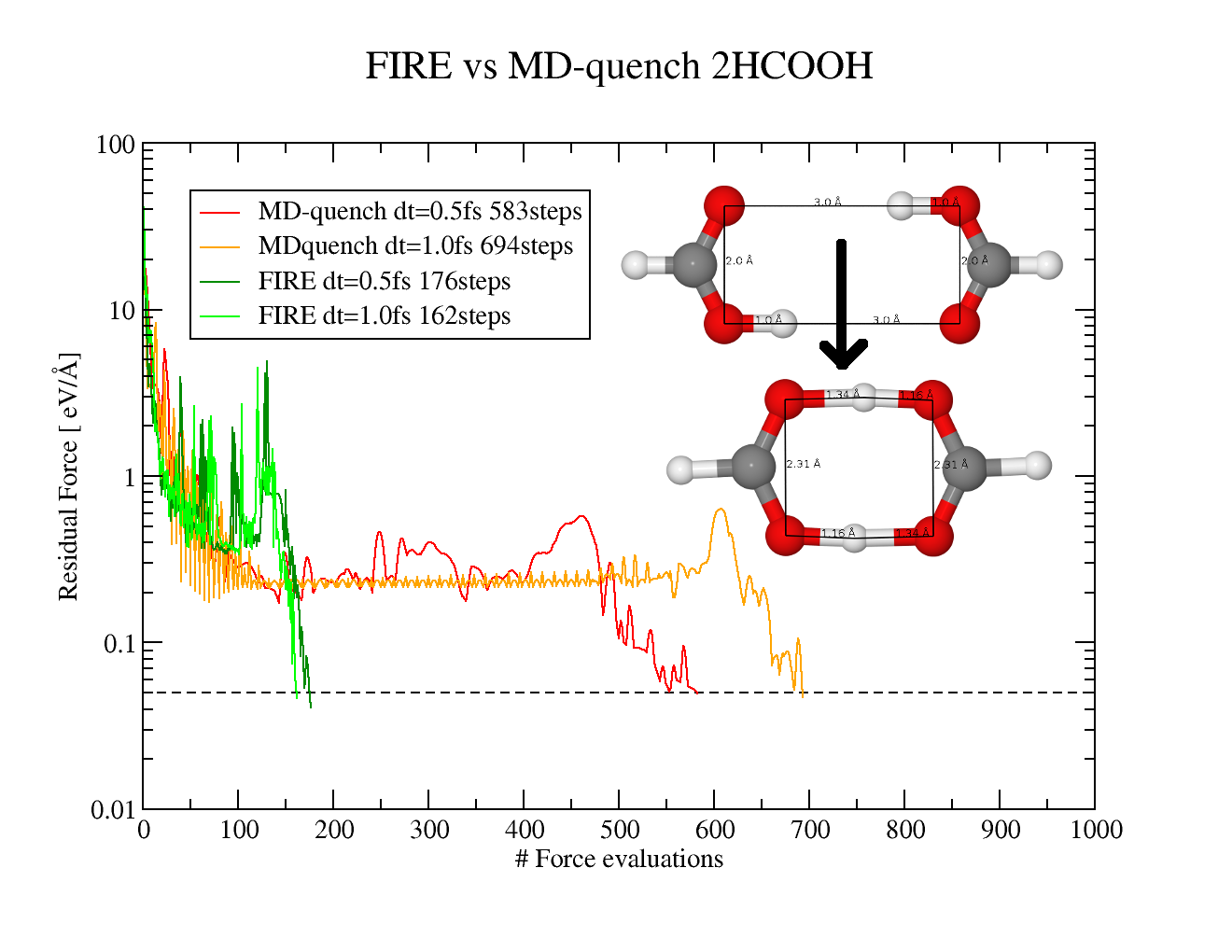
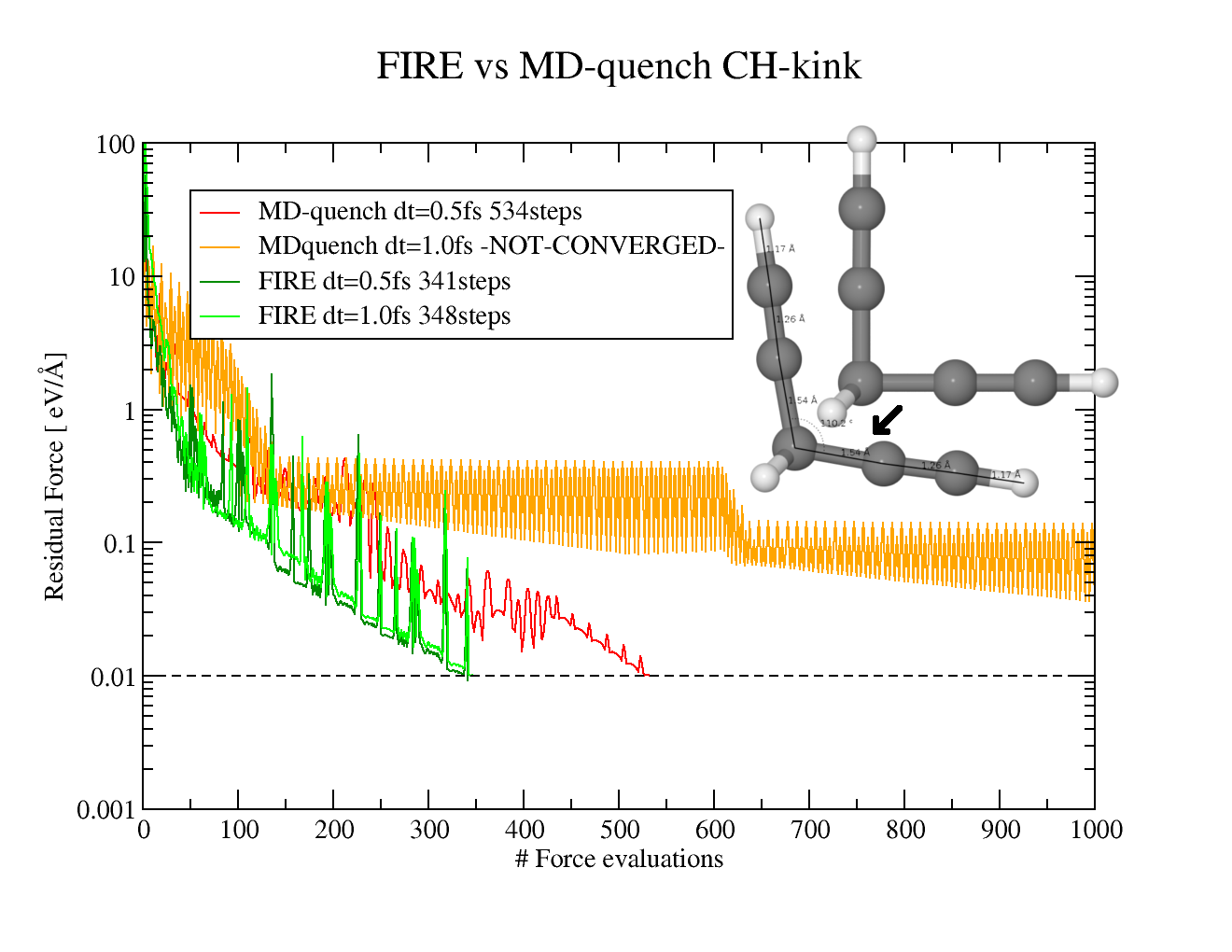
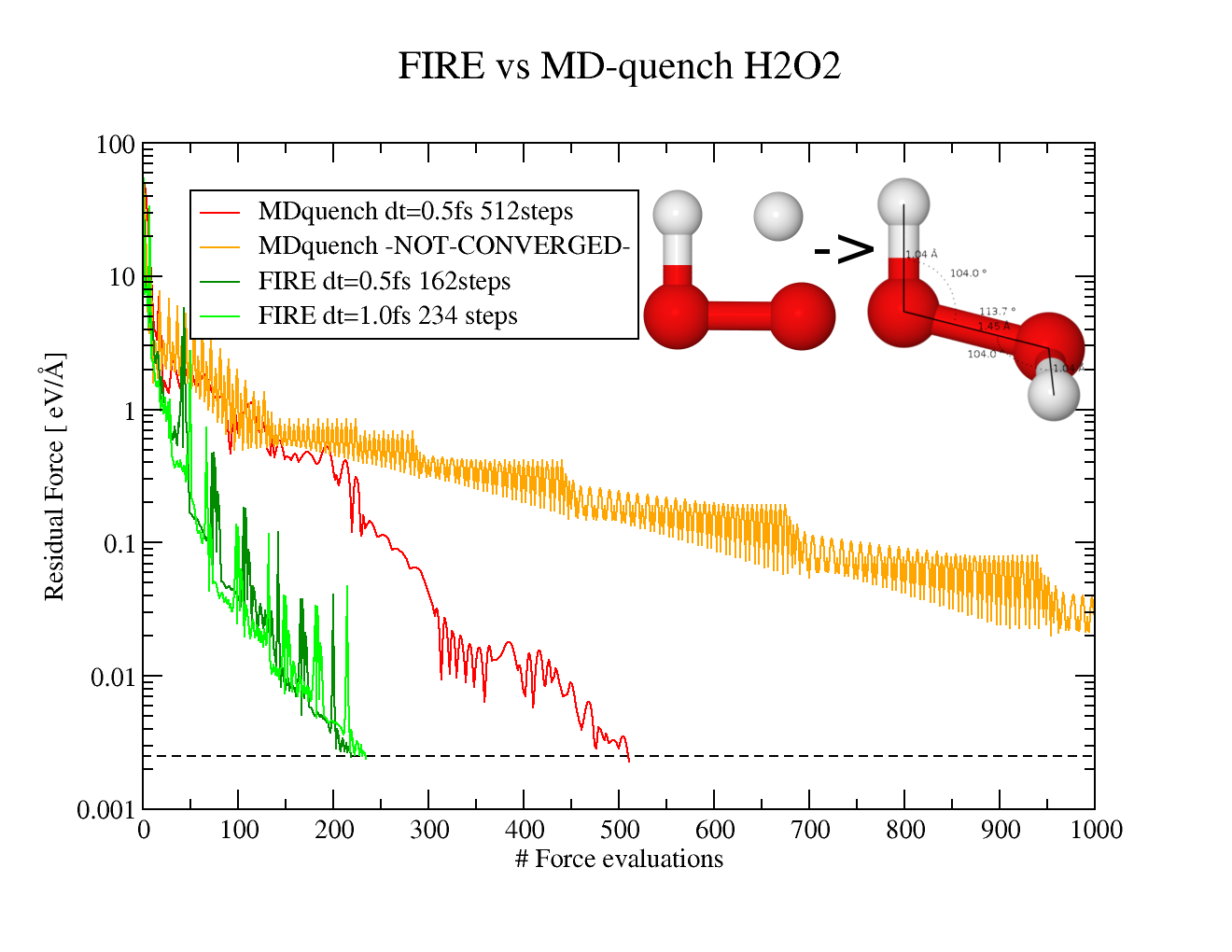
FIRE minimization

FIRE ( iquench = -6 ) is molecular dynamics based minimization technique, which use only gradient of the energy potential ( force ), but it often provides performance comparable or even superior to quasi-second-order Quasi-Newton algorithms such as BFGS. It differs from quenched molecular dynamics in the way how velocity is updated (see. pseudocode or references for more details). An other difference from standard quenched-MD (iquench=-1) is that mass of all atoms is set to 4.0 atomic units ( can be modified by FIRE_mass parameter) so Gold and Hydrogen atoms have the same inertia. In comparison to BFGS, FIRE algorithm is more robust ( and often also faster ) if the potential is far from being quadratic form, and in case of long narrow bend valley. For this reason it is well suited in case of soft degrees of freedom (such as dihedral angles, intermolecular electrostatic forces, hydrogen bond etc.)

Settings

Default parameters of FIRE algorithm are good for most of the cases and it is not necessary to set them manually. The only parameter which should be set in fireball.in is time step dt = 0.5 - 1.0 femtosecond.

In case you want to try your luck and play with the parameters of algorithm it is optionally possible to provide file 'FIRE.optional' of the folowing format (with default parameters as examples): 

1.1  ! FIRE_finc   ... increment time step if dot(f,v) is positive
0.5  ! FIRE_fdec   ... decrement time step if dot(f,v) is negative
0.1  ! FIRE_acoef0 ... coefficient of skier force update 
0.99 ! FIRE_falpha ... decrementarion of skier force compoenent acoef if projection dot(f,v) is positive
5    ! FIRE_Nmin   ... currently not used
4.0  ! FIRE_mass   ... mass of atoms

Pseudo Code

  1. Evaluate force
  2. Evaluate projection of force to velocity vf = dot(v,f); vv = dot(v,v); ff = dot(f,f);
  3. if (vf<0)
    • v=0
    • FIRE_dt = FIRE_dt * FIRE_fdec
    • FIRE_acoef = FIRE_acoef0
  4. else if ( vf>0 )
    • cF = FIRE_acoef * sqrt(vv/ff)
    • cV = 1 - FIRE_acoef
    • v = cV * v + cF * f
    • FIRE_dt = min( FIRE_dt * FIRE_finc, FIRE_dtmax )
    • FIRE_acoef = FIRE_acoef * FIRE_falpha
  5. MD step using leap-frog
    • v = v + (dt/FIRE_mass) * f
    • position = position + FIRE_dt * v

References

  1. Bitzek, E., Koskinen, P., Gähler, F., Moseler, M. & Gumbsch, P. Structural relaxation made simple. Phys. Rev. Lett. 97, 170201 (2006).
  2. Eidel, B., Stukowski, A. & Schröder, J. Energy-Minimization in Atomic-to-Continuum Scale-Bridging Methods. Pamm 11, 509–510 (2011).
  3. FIRE: Fast Inertial Relaxation Engine for Optimization on All Scales

Results